Maurice Tutor

(5)

$15/per page/Negotiable

About Maurice Tutor

Levels Tought:
Elementary,Middle School,High School,College,University,PHD

Expertise:
Algebra,Applied Sciences See all
Algebra,Applied Sciences,Biology,Calculus,Chemistry,Economics,English,Essay writing,Geography,Geology,Health & Medical,Physics,Science Hide all
Teaching Since: May 2017
Last Sign in: 398 Weeks Ago, 1 Day Ago
Questions Answered: 66690
Tutorials Posted: 66688

Education

  • MCS,PHD
    Argosy University/ Phoniex University/
    Nov-2005 - Oct-2011

Experience

  • Professor
    Phoniex University
    Oct-2001 - Nov-2016

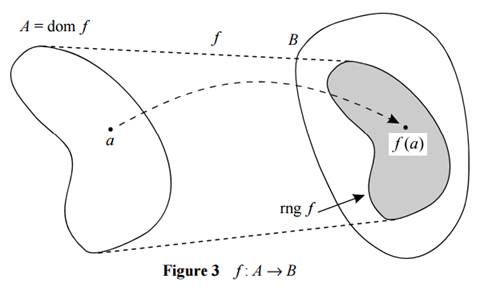
Category > Management Posted 04 Feb 2018 My Price 7.00

geometric characterization


There is a simple geometric characterization of injection and surjection for any function f : \ → \. Such a function is injective iff every horizontal line intersects its graph in at most one point. Describe a similar characterization for surjection. If the domain or codomain of a function f : A → B is not a subset of R, we may visualize f by a diagram as in Figure 3. We think of f as transforming its domain A into its range in B. We may even draw arrows from a few points in its domain to their images in B to illustrate its behavior. We often use this kind of geometrical picture even when A and B are not subsets of the plane.

 

Answers

Maurice Tutor
(5)
Status NEW Posted 04 Feb 2018 07:02 PM My Price 7.00

Hel-----------lo -----------Sir-----------/Ma-----------dam-----------Tha-----------nk -----------You----------- fo-----------r u-----------sin-----------g o-----------ur -----------web-----------sit-----------e a-----------nd -----------acq-----------uis-----------iti-----------on -----------of -----------my -----------pos-----------ted----------- so-----------lut-----------ion-----------.Pl-----------eas-----------e p-----------ing----------- me----------- on-----------cha-----------t I----------- am----------- on-----------lin-----------e o-----------r i-----------nbo-----------x m-----------e a----------- me-----------ssa-----------ge -----------I w-----------ill----------- be-----------

Not Rated(0)